Lenguajes Y Automatas 1: La jerarquia de la Gramatica

miércoles, 26 de febrero de 2020

Sea un lenguaje L definido por al menos una gramática G que cumple:

Si todas las producciones de G tienen la forma ó 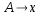donde A y B son simbolos no terminales y x es un terminal; entonces G se dice que es una gramática regular y L es un lenguaje regular o de tipo 3.
Si todas las producciones de G tienen la forma 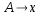donde x es una combinación de símbolos terminales y no terminales, entonces G se dice que es una gramática libre de contexto y L es un lenguaje libre de contexto o de tipo 2.
De ser las producciones de G de la forma donde A es un símbolo no terminal cualquiera, x, y, y z son combinaciones de terminales y no terminales, tales que x e y pueden ser cadenas vacías; entonces se dice que G es una gramática dependiente del contexto y L es un lenguaje dependiente del contexto o lenguaje de tipo 1.
Si ninguna de las gramáticas de L cumple las propiedades anteriores entonces se dice que es un lenguaje sin restricciones, recursivamente enumerable o de tipo 0.