6.3 - Lenguajes aceptados por la MT.

De acuerdo a la clasificación de los lenguajes formales realizada por el norteamericano Avram Chomsky, la Máquina de Turing acepta los lenguajes más generales, o tipo cero (0), también llamados lenguajes recursivamente enumerables.

Un lenguaje recursivamente enumerable es un lenguaje formal para el cual existe una máquina de Turing que acepta y se detiene con cualquier cadena del lenguaje, pero que puede parar y rechazar, o bien iterar indefinidamente, con una cadena que no pertenece al lenguaje. Todos los lenguajes, regulares, independientes de contexto, dependientes de contexto y recursivos son recursivamente enumerables.

Una cadena ω∈A^*, es aceptada por una MT, si comienza en el estado e0, con la cabeza de lectura/escritura en el símbolo más a la izquierda, luego de leer toda la cadena ω, llega a un estado e_f∈F. El lenguaje aceptado por MT, es el conjunto de todas las cadenas que son aceptadas por MT:

EJEMPLO:

L(MT)={ω / e_0 ω ⊢*α_1 e_f α_2 y e_f∈F y α_1,α_1 ∈C^* y ω∈A^* }

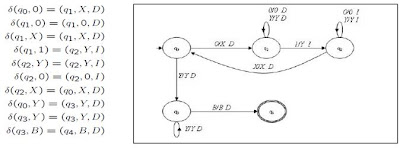
Tenemos por ejemplo una MT que reconoce el lenguaje {0^n 1^n:n≥1}. Las transiciones de la máquina se representan como sigue:

Se evalúa la cadena w = 1100, arrojando el siguiente resultado:

Otras cadenas también aceptadas por esta MT son 11110000, 10, 11111110000000.