Ejercicio Maquina de Turing 2

• DISEÑAR UNA MAQUINA DE TURING QUE CALCULA EL NUMERO CONSECUTIVO DE UN NUMERO DADO EN BINARIO

Vamos a considerar tres estados:

$$q_0,q_1,q_2$$

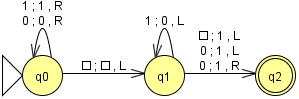
• Inicialmente, la MT está en el estado q₀ con la cabeza señalando la primera cifra del número.
  La MT recorre todo el número para ver si es par o impar sin modificar su cinta.
  
  $$\delta (q_0,0)=(q_0,0,R)$$
  $$\delta (q_0,1)=(q_0,1,R)$$
• Notemos que, por ahora, la MT se detiene al llegar al primer símbolo en blanco a la derecha del número.
  La MT vuelve a la anterior casilla (último número). Si es un 0, lo cambia por un 1 y pasa al estado final que es q₂ . Para hacer esto usaremos el estado q₁ :
  
  $$\delta (q_0,B)=(q_1,B,L)$$
  $$\delta (q_1,0)=(q_2,1,R)$$
• Si el número es impar, la MT no ha cambiado el último número, pero está en el estado q₁ . Tiene que cambiar todos los 1's consecutivos que haya de derecha a izquierda.
  
  $$\delta (q_1,1)=(q_1,0,L)$$
• Por ahora, la MT se para cuando llega al primer 0 (de derecha a izquierda) ó en un símbolo en blanco. Si es un 0, lo cambia por un 1 y el proceso finaliza:
  
  $$\delta (q_1,0)=(q_2,1,L)$$
  (Hemos escrito un desplazamiento a la izquierda, pero esto no tiene importancia ya que la MT ha llegado al estado final).
• Si lo que señala la cabeza es un blanco en vez de un 1, tiene que cambiarlo por un 1 y finalizar el proceso.
  
  $$\delta (q_1,B)=(q_2,1,L)$$

El diagrama de la máquina es